Future Value Example 1abc

Future Value - EXAMPLE 1a

How much should you deposit monthly starting on August 16, 2011, if you wanted to have $10,000.00 after 4 years? The current interest rate is 8.25% compounded monthly.

Solve Solve The Amount you must deposit per month.

action

Type

Select

Schedule of monthly deposits in the Heading field. This heading will appear at the top of the screen when the amortization table is generated. Use the TAB key or use the mouse to move to the next field.

8-16-2011 for the Beginning Date.

To enter the date in faster, click on the Calendar icon beside the field and then select the year, month and date.

8-16-2011 for the First Deposit Date.

0 in the Initial Investment field

8.25 in the Interest Rate field. The interest rate that you enter should always be the annual interest rate.

Note that the Effective Rate will automatically be calculated and displayed (see Glossary for definition).

Note: Since we are making monthly deposits, make sure the deposit frequency

is set to monthly.

4 in the Period field.

Years in the frequency if not already set to Years.

the Arrow button beside the Compounding Frequency field to show a list of

possible compounding frequencies.

You could type 48 and select the months, since 4 years is the equivalent of 48 moth.

Press

button beside the Deposit Amount field.

The monthly computed mortgage payment is $176.55.

Check your screen with the one illustrated below.

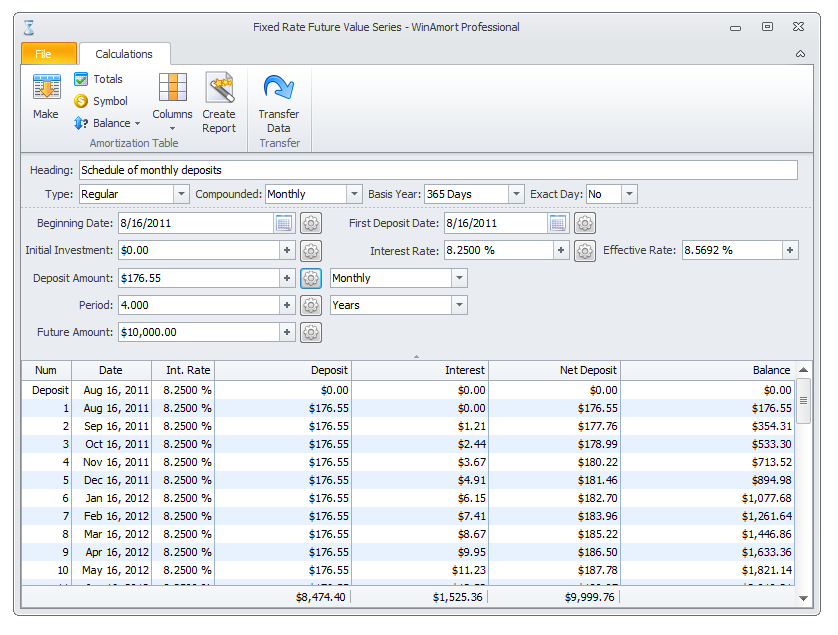
Future Value Example 1

Notice that the totals line in the table shows the end Net Deposit amount of $9,999.76.

The Net Deposit is short $0.24 cents. This is a result of rounding errors. If you were to click the compute button beside the Future Amount

field you will get the exact total or you can select the Balance button at the top or right click the table to bring up the Balance options.

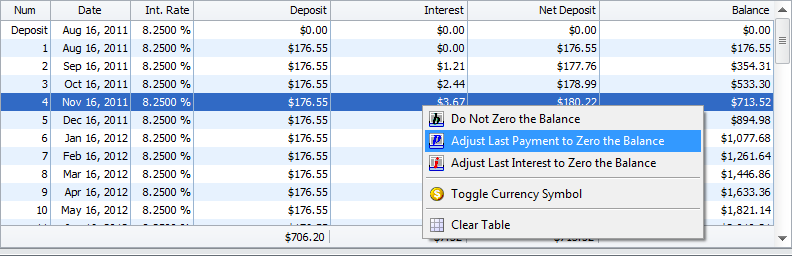
Future Value Balance Adjustment

You can select to adjust the final monthly payment or the Interest portion and $0.24 cents will be added to make the final total exactly $10,000.00

A line will also be added under the table totals indicating that the last Deposit Amount or Interest Amount has been increased by $0.24 to adjust

for rounding.

Future Value - EXAMPLE 1b

Suppose that you could increase the monthly amount you calculated in the last example by 10% every year. How much would cumulate at the end of the 4th year?

Solve Solve The Future Value at the end of the 4th year.

This example is now a Percent Step calculation. When you change the TYPE field to Percent Step,

the form will change by adding 3 extra fields that we can now use.

action Enter in the data as you seem necessary and compute the answer. Once completed,

you can verify your Form with the one illustrated below.

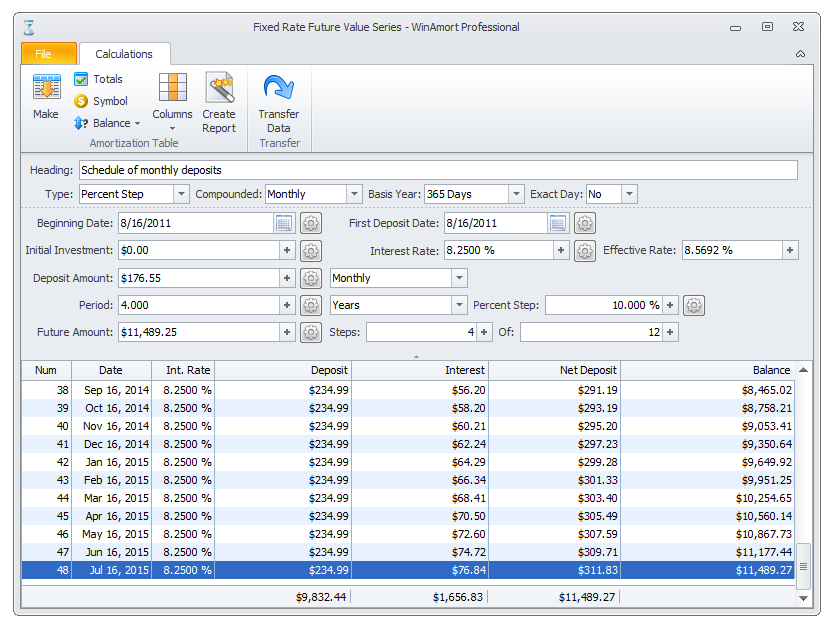
Future Value - with Percent Step

Notice that the Deposit Type Field shows “Percent Step.” Stepping was first introduced in the Mortgage and Loans Form.
It is still the same; recall that the feature allows gradual increases, at set intervals to be taken into account.

Press

button beside the Future Value field.

The Future value amount is $11,489.25

Therefore, by increasing your monthly amount by 10 percent every year you would have an additional $1,489.25 in savings. Why would you do this? One explanation is that you are able to increase your savings since your salary increases every year, or that you are keeping up with the inflation rate. With the previous example we did a “What if” scenario, where you are able to increase your monthly deposits over a period of time.

Future Value - EXAMPLE 1c

“What if”... you only needed to save $10,000, but could still increase your monthly payments by 10%. How much would you need to deposit monthly?

Solve Solve The Monthly Deposit amount.

This can be determined very easily. Just change the $1,489.25 value in the Future Value field back to $10,000.

Press

button beside the Deposit field.

The Future value amount is $153.67

This value now represents the starting amount of money you must deposit for the

next 12 months, in order to accumulate $10,000 in 4 years.

When you click the compute button, a new table is automatically generated. If you scroll down the table,

you can see the new monthly deposits amounts of $153.67 for the first 12 months which than increases

by 10% the second year and again for the 3rd and 4th years.

The values are:

$153.67

$169.04

$185.94

$204.53

For an Annuity based calculation in more details, see the next example.

Help URL: http://www.yourdomain.com/help/index.html?future_value_example_1.htm

Future Value Example 1abc					Future_Value_Example_1 Dear Support Staff,
Future Value Example 1abc